På sidan ”Rejewskis första bragd” (RFB) har jag beskrivit hur Marian Rejewski lyckades lista ut alla detaljer i den militära versionen av Enigma. Polackerna kunde i och med detta producera egna kompletta Enigma-maskiner.
Arbetet var långt ifrån avslutat bara för att man hade tillgång till maskinerna. För att dekryptera meddelanden behövde man komma på metoder för att ta reda på maskinens dagliga inställningar. Inställningarna distribuerades i pappersform inom den tyska krigsmakten.
Förutsättningar
Tyskarna visste naturligtvis redan från början att deras kryptering med Enigma var tvunget att tåla att enstaka maskiner föll i fiendens händer. Därmed krävdes nyckelhanteringar, i form av dagliga inställningar av maskinen, som hölls hemliga. De dagliga inställningarna skickades ut månadsvis till alla användare av Enigma.
För att åstadkomma metoder för att ta fram de dagliga inställningarna hade Rejewski samma förutsättningar som han hade innan sin första bragd, plus att han nu förstås hade kopior av Enigma till sitt förfogande. Han hade alltså bland annat:
- Tillgång till maskinens användarmanual. Därmed visste han Tyskarnas arbetsmetoder.
- Två månadsförteckningar över de dagliga inställningarna.
- Alla avlyssnade meddelanden från de två månaderna i klartext.
- Massvis av avlyssnade meddelanden insamlade under andra dagar.
Dagliga inställningar
Jag vill åter påpeka att jag förutsätter att läsaren redan skaffat sig kunskap om hur Enigma fungerar. Här koncentrerar vi oss på Enigmas ur ett matematiskt perspektiv. För en grundligare genomgång rekommenderar jag beskrivningen i RFB. Dock gör vi har en kort repetition av vad som är relevant för ”andra bragden”.
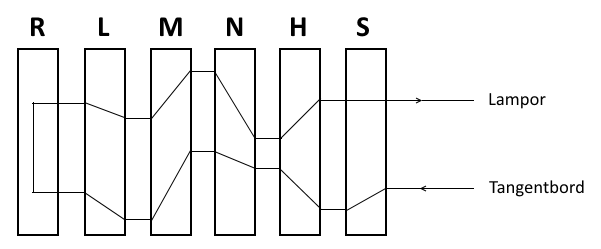
Följande bild visar Enigma ur ett logiskt permutationsperspektiv:
Från tangentbordet leds signalen genom permutationerna S, H, N, M, L för att sedan permutationsreflekteras i R och ledas tillbaka genom L, M, N, H, S och slutligen visa den krypterade signalen genom att tända en lampa på lampbordet.
De olika blocken i bilden är:
- S är korskoppling av sex bokstavspar. Övriga bokstäver passerar opåverkade genom S. S skulle till exempel kunna ha följande cykelform: (A)(BY)(C)(D)(ES)(F)(G)(HJ)(IM)(K)(L)(N)(OR)(P)(Q)(T)(U)(VZ)(W)(Z)
- H är den numer kända ingångspermutationen. Som vi såg i RFB är H enhetspermutationen I och den tillför därmed inget till krypteringen. I fortsättningen struntar vi helt i H.
- N, M och L är de tre rotorhjulen med numer kända permutationer. N är det snabbast roterande hjulet som stegar ett steg fram för varje tangenttryckning. M är näst snabbast och L långsammast.
- R är en numer känd permutation.
Vi kan uttrycka Enigmas totala permutation som:
SNMLRL^{-1}M^{-1}N^{-1}S^{-1}Ekvationen ovan stämmer visserligen men den tar ingen hänsyn till rotorhjulens rörelse och ej heller till de dagliga inställningarnas påverkan. Det kommer vi senare i detta dokument att ta hänsyn till men vi börjar med att klarlägga vilka de dagliga inställningarna är:
- Hjulordning. Det vill säga vilken ordning rotorhjulen är placerade i maskinen. Detta var för det mesta, åtminstone de första åren, känt eftersom hjulordningen byttes så sällan som en gång per kvartal. Hur som helst kunde det vissa dagar behöva bestämmas.
- Hjulens startposition. Vart och ett av de tre rotorhjulen kunde ju ställas i 26 olika positioner vid meddelandets start.
- Hjulens ringinställningar. Även ringinställningen kunde göras i 26 olika positioner. Ringinställningen på Enigma-hjulen förskjuter hjulets ”spaghettikopplingar” i förhållande till övriga delar av hjulet. Ringinställningarnas viktigaste funktion är att de snabbare hjulens triggning av långsammare hjul förskjuts i förhållande till hjulets permutation.
- Korskopplingarna. Det vill säga S permutationen.
Rejewski utvecklade metoder för att dagligen ta reda på inställningarna. Jag redovisar metoderna i tre avsnitt
- Gallermetoden (Grill method). Det klart största och mest avancerade avsnittet som bestämmer:
- Korskopplingarna S
- Vilket hjul som sitter i position N (om det behövs)
- N:s startposition
- Uttömmande prövning av Q. Q är en sammanskrivning av MLRL^{-1}M^{-1}. Metoden bestämmer:
- Vilka hjul som sitter i positionerna M och L
- M:s och L:s startposition
- ANX-metoden. Uttömmande prövning som bestämmer:
- Rotorhjulens ringinställningar.
Gallermetoden
Uttömmande prövning av Q
ANX-metoden
Avslutning