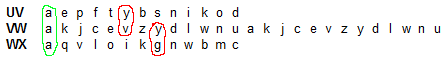Marian Rejewski avslöjade hur de interna kopplingarna i rotorhjulen och reflektorn hos den militära varianten av Enigma var gjorda. Med hjälp av matematik, spionage och nästan obegränsad slughet gjorde Rejewski en av de mest imponerande insatserna i kryptohistorien. Jag har valt att kalla prestationen Rejewskis första bragd.
Sammantaget utgjorde de Polska insatserna under trettiotalet grunden för det arbete som så förtjänstfullt fortsatte i Bletchley Park under kriget. Polackerna lyckades konstruera kopior av Eniga som överlämnades, tillsammans med vunnen kunskap, till Engelsmännen och Fransmännen strax före kriget.
En förutsättning för att kunna ta till sig materialet i detta dokument är kunskap om hur Enigma fungerar. Det finns gott om bra beskrivningar av Enigma såväl på nätet som i litteraturen.
Förutsättningar
I början av trettiotalet var delar av den militära versionen av Enigma fortfarande okända. Visserligen var principen för maskinen känd men den elektriska kabeldragningen inom ingångskopplingen, rotorhjulen och reflektorn var ännu en Tysk hemlighet.
Rejewski hade tillgång till den kommersiella versionen av Enigma. Den stora skillnaden mellan denna och den militära var, förutom nämnda kabeldragningskillnad, att den kommersiella saknade korskopplingar vid ingång till och utgång från maskinen.
Genom Franskt spionage hade Rejewski dessutom tillgång till maskinens användarmanual. Med andra ord visste han vilka inställningar som gjordes dagligen samt hur operatören agerade vid sändande av ett meddelande. Han visste därmed att Tyskarna först ställde in maskinen efter instruktioner som gällde för alla meddelande samma dag och därefter kodade en slumpvis framtagen trebokstavskod, som bara gällde detta meddelande, med Enigma. Han kodade därefter samma trebokstavskod igen. Därefter ställde han in sina Enigmahjul efter de tre slumpade bokstäverna. De sex krypterade bokstäverna inledde det krypterade meddelandet som sändes. Mottagaren som ställt in maskinen med samma dagliga inställningar och dekrypterade de första sex bokstäverna. Då fick han fram de tre bokstäverna dubbelt och ställde in sina hjul efter dessa innan han dekrypterade resten av meddelandet. Upprepandet av meddelandekoden gjordes för att undvika en felinställning av hjulen vilket skulle göra meddelandet oläsligt. Kryptologiskt var detta förfarande förkastligt vilket Rejewski naturligtvis insåg och utnyttjade.
Det Franska spionaget hade dessutom försett Polackerna med två månadsförteckningar över de dagliga inställningarna. Dessa månadsförteckningar var från olika kvartal vilket innebar att hjulordningen var olika eftersom samma hjulordning användes i ett kvartal och byttes därefter.
Rejewski hade tillgång till massvis av avlyssnade, krypterade, meddelanden insamlade under många dagar. Han hade bland annat meddelande för dagarna de månader då de dagliga inställningarna var kända.
Grupp och permutationsteori
Den matematik som användes av Rejewski kallas grupp- och permutationsteori. Jag går här igenom de begrepp och teorem som kommer att användas senare i dokumentet. Jag kommer inte att bevisa teoremen. Däremot kommer jag resonera lite kring deras rimlighet som räkneregler. För att förenkla lite använder jag mig av ett sexbokstavsalfabet bestående av A, B, C, D, E och F.
Definition av permutationen P.
Permutationen P är en ett till ett överföringsfunktion från en grupp bestående av bokstäverna i alfabetet till en annan grupp bestående av bokstäverna i alfabetet. I vårt fall kan P till exempel beskrivas med följande mappning:
P : \begin{pmatrix} A & B & C & D & E & F \\ \Downarrow & \Downarrow&\Downarrow&\Downarrow&\Downarrow&\Downarrow\\ C & E & D & F & B & A \end{pmatrix}Permutationen P innebär alltså att A överförs till C, B överförs till E och så vidare.
Normalt sett skrivs permutationer utan pilarna:
P : \begin{pmatrix} A & B & C & D & E & F \\ C & E & D & F & B & A \end{pmatrix}Permutationen P kan skrivas på kortare cyklisk form:
P : (ACDF)(BE)vilket skall tolkas som att:
P: A \Rightarrow C \Rightarrow D \Rightarrow F \Rightarrow A samt B \Rightarrow E \Rightarrow B.
En permutations cykliska struktur
Vi har tre permutationer P, Q och R sådana att:
- P: (ACDF)(BE)
- Q: (AFD)(BEC)
- R: (AF)(BDEC)
Vi säger att P och R har samma cykliska struktur eftersom båda består av en fyrabokstavscykel och en tvåbokstavscykel. Q däremot har en annan cyklisk struktur bestående av två trebokstavscykler.
Begreppet cyklisk struktur kommer att vara väldigt viktigt längre fram i dokumentet.
Produkt av permutationer
Med produkten PQ av två permutationer P och Q menar vi den sammansatta permutationen vi får när först P och därefter Q får verka på en grupp. Vi får till exempel:
- P: (ACDF)(BE)
- Q: (A)(BCD)(EF)
- PQ: (ADECBF)
Lägg märke till att produkten PQ vanligtvis inte ger samma permutation som produkten QP
Invers permutation och enhetspermutationen
Inversa permutation P^{-1} definieras unikt av P genom att den återför eller reverserar permutationen P. Om vi till exempel har P: (ACDF)(BE) så ger det inversen P^{-1}: (AFDC)(BE).
Produkten PP^{-1} blir alltid (A)(B)(C)(D)(E)(F) vilket vi kallar enhetspermutationen I. Enhetspermutationen är alltså en överföring av alla bokstäver till sig själv. Vi får följande räknergler:
- PP^{-1} = I
- PI = P = IP
Teoremet om konjugerade permutationer
Två permutationer K och F kallas konjugerade om de har samma cykliska struktur.
Om K och F är konjugerade kan vi finna minst en permutation P så att F = PKP^{-1}. Lägg märke till att det kan finnas flera permutationer P som löser ekvationen.
Dessutom gäller att om vi kan finna en permutation P sådan att F = PKP^{-1} så är permutationerna F och K konjugerade.
Vi skall som sagt inte bevisa teoremet men vi kan ändå rättfärdiga det genom följande tolkning:
- I vänsterledet permuteras gruppen av F.
- I högerledet sker samma sak fast i tre faser. För transfererar P bokstäverna i F:s struktur till motsvarande bokstäver i K:s struktur. Därefter permuteras gruppen av K strukturellt likadant som av F. Till sist transfereras bokstäverna i K:s struktur tillbaka till bokstäverna i F:s struktur.
Teoremet är viktigt för fortsättningen och kommer att göra underverk senare i detta dokument. Testa gärna med lite exempel om teoremet är svårt att ta till sig och mitt resonemang känns otillräckligt.
Definition av Enigma Permutation
En permutation som endast består av tvåbokstavscykler kallar jag en Enigma-permutation. Permutationen X: (AF)(BD)(CE) är en Enigma Permutation. Som vi senare skall se kommer sig namnet av att Enigma utför just denna typ av permutationer. I övrig litteratur kallas Enigma-permutationen oftast för transposition.
Teoremet om produkt av Enigma Permutationer.
Produkten av två Enigma permutationer X och Y innehåller ett jämnt antal cykler av samma längd. Vi får till exempel:
- X: (AF)(BD)(CE)
- Y: (AE)(BC)(DF)
- XY: (ADC)(BFE)
I exemplet fick produkten två trebokstavscykler.
Teoremet gäller omvänt också. En permutation bestående av ett jämnt antal cykler av samma längd kan alltid betraktas som en produkt av två Enigma-permutationer.
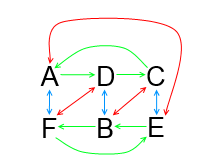
Beviset hoppar jag över även här. Dock motiverar jag teoremet med hjälp av en graf. Låt X och Y från ovan representeras av blå respektive röda dubbelriktade pilar i följande graf:
Dubbelriktade pilar använder jag eftersom att X och Y är Enigma-permutationer.
Om nu X överför A till F måste Y antingen föra tillbaka F till A eller som i detta fall till en ny bokstav D. X måste därefter överföra D till ytterligare en ny bokstav B och så vidare. För eller senare måste Y överföra tillbaka till A, i detta fall händer det från E.
Nu är det dags att rita in produkten XY med gröna pilar. Läsaren kan själv kontrollera att jag ritat pilarna rätt. Av bilden framgår att produkten kommer att bilda två lika långa cykler, en i övre och en i nedre raden.
Enigma
Jag förutsätter att läsaren skaffat sig kunskap om Enigma på förhand. Det finns gott om beskrivningar på nätet och i litteraturen. Jag kommer i detta kapitel koncentrera mig på Enigmas logiska funktion ur ett matematiskt perspektiv. De mekaniska och elektriska finesserna får inhämtas på annat håll.
Vid tiden för Rejewskis första bragd var Enigma utrustad med endast tre rotorhjul. Dessa tre kunde skifta plats och gjorde så med jämna mellanrum. Vidare användes sex korskopplingspar av Enigma-operatörerna.
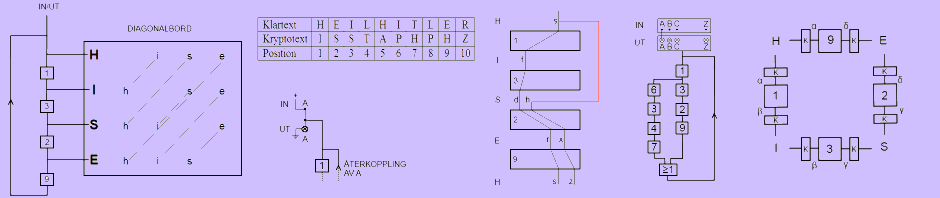
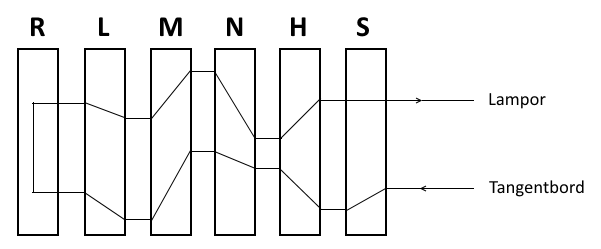
Följande bild visar Eniga ur ett logiskt permutationsperspektiv:
Från tangentbordet leds signalen genom permutationerna S, H, N, M, L för att sedan permutationsreflekteras i R och ledas tillbaka genom L, M, N, H, S och slutligen visa den krypterade signalen genom att tända en lampa på lampbordet.
De olika blocken i bilden är:
- S är korskoppling av sex bokstavspar. Övriga bokstäver passerar opåverkade genom S. S skulle till exempel kunna ha följande cykelform: (A)(BY)(C)(D)(ES)(F)(G)(HJ)(IM)(K)(L)(N)(OR)(P)(Q)(T)(U)(VZ)(W)(Z)
- H är en okänd permutation av okänd struktur. H är statisk eftersom den inte roterar vid tangenttryckningar. Permutationen var känd för den kommersiella versionen av Enigma.
- N, M och L är de tre rotorhjulen med okända permutationer av okänd struktur. N är det snabbast roterande hjulet som stegar ett steg fram för varje tangenttryckning. M är näst snabbast och L långsammast.
- R är en okänd permutation vars struktur dock är känd. R är en Enigma-permutation.
Vi kan uttrycka Enigmas totala permutation som:
SHNMLRL^{-1}M^{-1}N^{-1}H^{-1}S^{-1}
Vi behöver en hjälppermutation P och dess invers för att kunna ta hänsyn till att rotorhjul N stegar fram vid varje tangenttryckning:
P = (ABCDEFGHIJKLMNOPQRSTUVWXY)
P^{-1} = (AZYXWVUTSRQPONMLKJIHGFEDCB)
Om vi nu kallar första bokstavens kryptering A, andra bokstavens kryptering B och så vidare samt låter rotorhjul N stega fram en position i inledningen av varje tangenttryckning fås följande permutationer:
- A = SHPNP^{-1}MLRL^{-1}M^{-1}PN^{-1}P^{-1}H^{-1}S^{-1}
- B = SHP^2NP^{-2}MLRL^{-1}M^{-1}P^2N^{-1}P^{-2}H^{-1}S^{-1}
- C = SHP^3NP^{-3}MLRL^{-1}M^{-1}P^3N^{-1}P^{-3}H^{-1}S^{-1}
- D = SHP^4NP^{-4}MLRL^{-1}M^{-1}P^4N^{-1}P^{-4}H^{-1}S^{-1}
- E = SHP^5NP^{-5}MLRL^{-1}M^{-1}P^5N^{-1}P^{-5}H^{-1}S^{-1}
- F = SHP^6NP^{-6}MLRL^{-1}M^{-1}P^6N^{-1}P^{-6}H^{-1}S^{-1}
Just nu ser det lite rörigt ut, väldigt mycket i ekvationerna är obekant. Det kommer dock klarna i nästa kapitel.
Vi kan, med hjälp av teoremet om konjugerade permutationer, konstatera att A, B C, D, E och F är Enigma-permutationer eftersom de kan skrivas på formen A = PRP^{-1} respektive B = PRP^{-1} och så vidare. Enigma-permutationsegenskapen kommer alltså från reflektorpermutationen. Observera att P nu används som förkortning till det som står till vänster om R i högerledet i ekvationerna ovan.
Kontrollera gärna sanningshalten i resonemanget genom att multiplicera det till vänster om R med det till höger om R i högerledet i ekvationerna ovan. Det bör gå att multiplicera ihop allt till enhetspermutationen I.
Vi kommer i senare kapitel utnyttja att A-F är Enigma-permutationer.
Högra hjulets permutation
Målet med Rejewskis analys var att avslöja det högra rotorhjulets permutation. Vi söker alltså N i ekvationerna ovan. Vi börjar med att avslöja vänsterledet i ekvationerna, det vill säga A, B, C, D, E och F. Avslöjandet görs i två steg, först tar vi reda på produkterna AD, BE samt CF och därefter används produkterna för att avslöja A, B, C, D, E och F.
Produkterna AD, BE och CF av vänsterleden
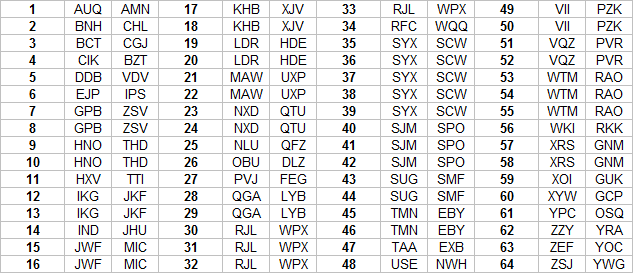
Rejewski hade som tidigare nämnts tillgång till avlyssnade meddelanden där han kände till hur de första sex tecknen hade producerats med hjälp av Enigmas daginställning och tre slumpmässiga bokstäver α, β och γ. Rejewski valde avlyssnade meddelanden från en dag med mycket trafik.
Tabellen visar de sex första uppsnappade tecknen från 64 meddelanden samma dag. Om vi börjar med att ta reda på permutationen AD så använder vi första och fjärde bokstaven i varje meddelande. Första meddelandet visar att såväl A som D omvandlar första bokstaven α av de tre slumpmässigt utvalda till a. Vi har därmed a \Leftrightarrow \alpha för såväl permutation A som D. Detta ger i sin tur att vi vet att a \Leftrightarrow a för produkten AD. På samma vis ger meddelande två b \Leftrightarrow \alpha för A och c \Leftrightarrow \alpha för D vilket i sin tur ger b \Rightarrow c för produkten AD. Vi upprepar förfarandet för alla meddelanden och får en väl vald dag reda på hela permutationen AD.
AD = (a)(s)(bc)(rw)(dvpfkxgzyo)(eijmunqlht)
Därefter utnyttjar vi på samma sätt resten av tabellen för att finna BE och CF
BE = (axt)(blfqveoum)(cgy)(d)(hjpswizrn)(k)
CF = (abviktjgfcqny)(duzrehlxwpsmo)
Lägg märke till att de tre produktpermutationerna innehåller ett jämnt antal cykler av samma längd precis som vi förväntar oss enligt teoremet om produkt av Enigmapermutationer.
Vänsterleden A, B, C, D, E och F
Även om vi nu vet produkterna AD, BE och CF finns det många många varianter av A, B, C, D, E och F som ger produkterna. AD kan fås genom 20 (2 gånger 10) varianter av A och D. BE kan fås genom 27 (3 gånger 9) varianter av B och E. CF kan fås genom 13 varianter av C och F. Kontrollera gärna med hjälp av produktpermutationerna ovan att detta stämmer.
Rejewski märke att de utvalda trebokstavskombinationerna inte var speciellt slumpmässiga. Vi har till exempel fem upprepningar av samma tre bokstäver som ger inledningen SYX SCW på meddelandet. Han antog att de Tyska operatörerna inte valde slumpmässigt alltid utan kanske använde tre intilliggande tangenter på Enigmas tangentbord eller kombinationer som abc, xyz eller aaa, bbb och så vidare.
Vi går vidare med att studera SYX SCW och ser vad det kan ge. Med hjälp av AD ekvationen ovan får vi s \Rightarrow a \Rightarrow s. Av BE ekvationen får vi y \Rightarrow a, x eller t \Rightarrow c. Av CF ekvationen får vi x \Rightarrow a, b, v, i, k, t, j, g, f, c, q, n eller y \Rightarrow w. Vi har nu sammanfattningsvis:
- α kan vara a
- β kan vara a,x,t
- γ kan vara a,b,v,i,k,t,j,g,f,c,q,n,y
Av dessa 27 kombinationer ser aaa ut att vara en bra kandidat för en icke slumpmässig trebokstavskombination. Om vi antar att aaa är korrekt faller kvickt viktiga bitar på plats för permutationerna A-F. Till exempel ger ju valet x \Rightarrow a \Rightarrow w för CF automatiskt såväl C som F:
- C = (ax)(bl)(vh)(ie)(kr)(tz)(ju)(gd)(fo)(cm)(qs)(np)(yw)
- F = (xb)(lv)(hi)(ek)(rt)(zj)(ug)(df)(oc)(mq)(sn)(py)(wa)
Permutationerna A, B, D och E får vi bara delar av:
- A = (as)
- B = (ya)(ct)(gx)
- D = (as)
- E = (ac)(tg)(xy)
Informationen kan användas för att lösa en del av meddelandetabellen. Därefter kan ytterligare en meddelandekod listas ut och mer av permutationerna klarnar.
Vi kan till exempel titta på WTM RAO som förekommer tre gånger. Med hjälp av AD ekvationen ovan får vi w \Rightarrow b eller c \Rightarrow r. Av de delar vi nu vet av B och E ekvationerna får vi t \Rightarrow c \Rightarrow a. C och F ekvationerna har vi ju så vi vet att m \Rightarrow c \Rightarrow o. Vi har nu sammanfattningsvis:
- α kan vara b,c
- β kan vara c
- γ kan vara c
Vi kan nu med god fog anta att den vanliga icke slumpmässiga meddelandekoden är ccc vilket betyder att A och D ekvationerna tillfogas ytterligare information.
Om vi går vidare med ytterligare meddelande löses ekvationerna A-F komplett. Kontrollera gärna att så är fallet. Vi har nu de sex ekvationerna A-F:
- A = (as)(br)(cw)(di)(ev)(fh)(gn)(jo)(kl)(my)(pt)(qx)(uz)
- B = (ay)(bj)(cr)(dk)(ei)(fn)(gx)(hl)(mp)(ow)(qr)(su)(vz)
- C = (ax)(bl)(cm)(dg)(ei)(fo)(hv)(ju)(kr)(np)(qs)(tz)(wy)
- D = (as)(bw)(cr)(dj)(ep)(ft)(gq)(hk)(iv)(lx)(mo)(nz)(uy)
- E = (ac)(bp)(dk)(ez)(fh)(gt)(io)(jl)(ms)(nq)(rv)(uw)(xy)
- F = (aw)(bx)(co)(df)(ek)(gu)(hi)(jz)(lv)(mq)(ns)(py)(rt)
Vi vet nu vänsterledens permutationer A, B, C, D, E och F och går vidare med högerleden.
Högerleden
Vi upprepar ekvationerna som beskriver den sammanlagda permutationen för de sex första bokstäverna i varje krypterat meddelande:
- A = SHPNP^{-1}MLRL^{-1}M^{-1}PN^{-1}P^{-1}H^{-1}S^{-1}
- B = SHP^2NP^{-2}MLRL^{-1}M^{-1}P^2N^{-1}P^{-2}H^{-1}S^{-1}
- C = SHP^3NP^{-3}MLRL^{-1}M^{-1}P^3N^{-1}P^{-3}H^{-1}S^{-1}
- D = SHP^4NP^{-4}MLRL^{-1}M^{-1}P^4N^{-1}P^{-4}H^{-1}S^{-1}
- E = SHP^5NP^{-5}MLRL^{-1}M^{-1}P^5N^{-1}P^{-5}H^{-1}S^{-1}
- F = SHP^6NP^{-6}MLRL^{-1}M^{-1}P^6N^{-1}P^{-6}H^{-1}S^{-1}
Rejewski hade från början ingen aning om korskopplingspermutationen S. Genom det Franska spionaget fick han dock tillgång till S under September och Oktober 1932 och betraktade därmed S som känd. För den dag då vänsterledens permutationer A, B, C, D, E och F beskrivs ovan hade S följande permutation:
S = (ap)(bl)(cz)(d)(e)(fh)(g)(i)(jk)(m)(n)(o)(qu)(r)(s)(t)(v)(w)(x)(y)
Även den statiska ingångspermutationen H var okänd. Rejewski visste visserligen hur H såg ut för den kommersiella versionen av Enigma och att denna inte var särskilt slumpmässig utan byggde på bokstävernas placering på tangentbordet. Han antog från början att H var den samma för den militära versionen men det visade sig vara fel. Han testade andra ”icke slumpmässiga” H utan framgång innan han till slut testade den allra enklaste permutationen, enhetspermutationen I, som visade sig rätt. Därmed betraktades även H som känd och nu kan ekvationerna skrivas om med kända permutationer överflyttade till vänsterleden:
- P^{-1}H^{-1}S^{-1}ASHP = NP^{-1}QPN^{-1}
- P^{-1}H^{-1}S^{-1}BSHP = NP^{-2}QPN^{-2}
- P^{-1}H^{-1}S^{-1}CSHP = NP^{-3}QPN^{-3}
- P^{-1}H^{-1}S^{-1}DSHP = NP^{-4}QPN^{-4}
- P^{-1}H^{-1}S^{-1}ESHP = NP^{-5}QPN^{-5}
- P^{-1}H^{-1}S^{-1}FSHP = NP^{-6}QPN^{-6}
För att göra ekvationerna lite mer lättlästa vi infört en ny permutation Q som bara är ett kortare skrivsätt för MLRL^{-1}M^{-1} och som ingår i alla ekvationerna.
Vänsterleden är ju som sagt kända och vi inför beteckningarna U, V, W, X, Y, Z på dem:
- U = NP^{-1}QPN^{-1}
- V = NP^{-2}QP^2N^{-1}
- W = NP^{-3}QP^3N^{-1}
- X = NP^{-4}QP^4N^{-1}
- Y = NP^{-5}QP^5N^{-1}
- Z = NP^{-6}QP^6N^{-1}
Vi kommer faktiskt bara behöva fyra av ekvationerna för att lösa N och beräknar därför bara U, V, W, X:
- U = (ax)(bu)(ck)(dr)(ej)(fw)(gi)(lp)(ms)(nz)(oh)(gt)(vy)
- V = (ar)(bv)(co)(dh)(fl)(gk)(iz)(jp)(mn)(qy)(su)(tw)(xe)
- W = (as)(bz)(cp)(dq)(eo)(fw)(gj)(hl)(iy)(kr)(mu)(nt)(vx)
- X = (ap)(bf)(cu)(dv)(ei)(gr)(ho)(jn)(ky)(lx)(mz)(qs)(rw)
Om vi nu multiplicerar de fyra översta ekvationerna parvis får vi tre ekvationer att jobba vidare med:
- UV = NP^{-1}(QP^{-1}QP)PN^{-1}
- VW = NP^{-2}(QP^{-1}QP)P^2N^{-1}
- WX = NP^{-3}(QP^{-1}QP)P^3N^{-1}
Lägg märke till att alla högerleden innehåller faktorn (QP^{-1}QP). Vi gör nu tricket att bryta ut (QP^{-1}QP) ur den första ekvationen och stoppa in i den andra. På samma vis gör vi med ekvation två och tre. Vi har därmed nu bara två ekvationer kvar:
- VW = NP^{-1}N^{-1}(UV)NPN^{-1}
- WX = NP^{-1}N^{-1}(VW)NPN^{-1}
UV, VW och WX känner vi ju till, bara att multiplicera ihop permutationerna ovan:
- UV = (aepftybsnikod) (rhcgzmuvqwljx)
- VW = (akjcevzydlwnu) (smtfhqibxopgr)
- WX = (aqvloikgnwbmc) (puzftjryehxds)
Vi har alltså nu två ekvationer med konjugerande permutationer. De två ekvationerna har dessutom samma ”överföringspermutationer” NP^{-1}N^{-1} och NPN^{-1}. För att lösa ekvationerna och därmed bestämma NPN^{-1} tycker jag det är snyggt att använda en metod med pappersremsor
Eftersom VW ingår i båda ekvationerna skriver jag båda dess trettonbokstavscykler dubbelt på vars en pappersremsa. Därefter skjuter jag en remsa med UV:s ena cykel utmed VW:s ena dubbelcykel och provar för varje steg om jag kan åstadkomma samma överföring genom att placera en remsa av någon av WX:s cykler under:
I första steget permuteras a till a för båda ekvationerna. Däremot permuteras y till v respektive g vilket gör att jag skjuter UV remsan vidare.
Så småningom hittar jag en position där alla bokstäver permuteras likadant i de två ekvationerna:
Ur bilden plockar vi nu:
NPN^{-1} = (ayuricxqmgovskedzplfwtnjhb)
Högerhjulets permutation får vi nu enkelt genom att skriva NPN^{-1} ovanför P i permutationen:
N: \begin{pmatrix} a & y & u & r & i & c & x & q & m & g & o & v & s & k & e & d & z & p & l & f & w & t & n & j & h & b \\ a & b & c & d & e & f & g & h & i & j & k & l & m & n & o & p & q & r & s & t & u & v & w & x & y & z \end{pmatrix}Om det verkade lite förvirrande kan man tänka så här: För någon bokstav i övre raden till exempel m kan vi få NPN^{-1} antingen genom att gå ett steg höger till g eller genom att ta omvägen ner med hjälp av N, ett steg höger med hjälp av P och slutligen upp med hjälp av N^{-1} .
Den permutation N som vi fått är bara en av 26 möjliga. Vi skulle kunna förskjuta raderna som gav N i förhållande till varandra och på så sätt få ett annat N. Detta motsvarar i verkligheten att vi inte vet vilken position högerhjulet sitter i.
Vi avslutar med att snygga till permutationen N genom att flytta om kolumnerna:
N:\begin{pmatrix} a&b&c&d&e&f&g&h&i&j&k&l&m&n&o&p&q&r&s&t&u&v&w&x&y&z \\ a&z&f&p&o&t&j&y&e&x&n&s&i&w&k&r&h&d&m&v&c&l&u&g&b&q \end{pmatrix}De andra hjulens permutationer
För att ta reda på de andra två hjulens permutationer fick Rejewski använda sig av uppsnappade meddelanden och korskopplingar från en dag i ett annat kvartal eftersom hjulordningen vid denna tid förändrades en gång var tredje månad. Därefter kunde även reflektorpermutationen R bestämmas. Rejewski har berättat att redan efter det att två hjul hade bestämts med metoden ovan kunde även tredje hjulet och reflektorn bestämmas med andra metoder.
Avslutning
Rejewskis prestation under senare delen av 1932 är en av de mer imponerande insatserna i kryptohistorien. En snyggare kombination av diskret matematik och logisk tänkande har jag svårt att föreställa mig. Jag är evigt tacksam att hans prestationers betydelse för läsandet av Nazitysklands krypterade meddelanden blev offentligt i tid så att han hann berätta om hur han utförde sina bragder.
Litteratur och Länkar
- Enigma – How the German mashine cipher was broken and how it was read by the allies in world war two. Wladyslaw Kozaczuk