Idéerna som låg till grund för det som brukar kallas ”The Turing Bomb” är bland det mest fascinerande jag någon gång stött på. Det är genialiska men samtidigt förbluffande enkla innovationer som bygger upp Bombens logik.
Min förhoppning är att jag här skall ge en språkligt och matematiskt enkel beskrivning som koncentrerar sig på ”tänket” i Bomben. Jag inleder med lite information om Enigma, Bomben och hur Bomben angriper svagheter hos Enigma. Därefter ägnas merparten av dokumentet åt att bit för bit tillföra Bomben logiska byggstenar.
Först lite om ”fienden”, Enigma.
Enigma
Enigma-maskinen behöver egentligen en helt egen beskrivning likt den jag gör här för Turing Bomb. Dock finns det inte utrymme här för att förklara allt om Enigma. Jag förutsätter att läsaren skaffat sig kunskap om Enigma på förhand. Det finns gott om beskrivningar på nätet och i litteraturen.
I det fortsatta resonemanget förutsätter vi en Enigma med tre aktiva rotorhjul och att det totalt finns fem hjul att välja bland. Vidare antar vi att tio korskopplingar(ty. steckers) används vid ingång till och utgång ur maskinen.
Några av Enigmas egenskaper vill jag ändå lyfta fram eftersom de är viktiga för Bombens konstruktion och arbetssätt:
- Enigma kan aldrig kryptera en bokstav till sig själv.
- Enigmas kryptering är ömsesidig. Detta betyder att om A krypteras till F för en viss Enigma-inställning krypteras F till A för samma inställning.
- Enigmas kryptering av en bokstav kan delas upp i tre delar. Först ingångskorskoppling, sedan rotordelen och till sist utgångskorskoppling.
Tredje punkten i listan förtjänar extra uppmärksamhet. Lägg märke till att ingångs- och utgångskorskopplingen är statiska i den meningen att de inte förändras av att Enigma stegar fram. I och med detta kan vi separera det som ändras under krypteringen, rotorpaketet, från det som bidrar med överlägset flest inställningskombinationer, korskopplingarna.
Bomben
Med Bomber avser vi de maskiner som byggdes under andra världskriget för bruk i bland annat Bletchley Park. Namnet Bomb var hämtat från maskinens Polska föregångare. Bomberna var elektromekaniska maskiner som efterliknade delar av Enigmas funktionalitet. Originalmaskiner finns tyvärr inte kvar och inte heller några ritningar är sparade. Däremot finns det en modern kopia som byggts med hjälp av viss dokumentation samt ögonvittnesuppgifter från de som använde eller var med i tillverkningen av maskinerna.
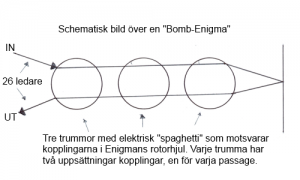
Bomben består av 36 Enigmor utan korskopplingar. Egentligen är det fel att de kallas Enigmor. Det är i själva verket tre trummor och reflektorutrustning som uppfyller funktionaliteten hos Enigmans rotordel. Inte heller finns det några inmatningstangenter eller indikationslampor på de enskilda Enigmorna. Istället ansluts kablar med 26 ledare, en för varje bokstav, för in och utmatning. Kablarna med sina 26 ledare kan sedan kopplas till en annan Enigma eller till inmatnings och avläsningsutrustning som är gemensam för hela Bomben. Lite slarvigt uttryckt kan vi säga att Bomben kan skicka insignaler till slingor av Enigmor för att sedan avläsa den totala utsignalen. Mer om detta senare i dokumentet.
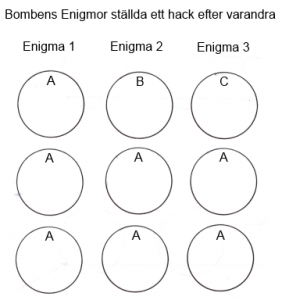Enigmorna konfigureras inför en bombkörning så att de ligger ett ”hack” efter varandra hela tiden. Första maskinen AAA, andra BAA, osv. När bomben tickat fram ett steg har första maskinen BAA, andra CAA, osv. En bombkörning består helt enkelt i att maskinen testar alla kombinationer av inställningar för den första Enigman. Samtidigt testas alla kombinationer av inställningar för den andra maskinen men den är hela tiden förskjuten ett steg i förhållande till den första. Nummer tre är naturligtvis förskjuten ytterligare ett steg o.s.v. För var och en av de 17576 (26*26*26) kombinationerna görs en elektrisk analys av utsignalerna från slingorna av Enigmor för att finna intressanta inställningar som stoppar maskinen. Stoppinställningarna blir då kandidater som är möjliga lösningar och får testas vidare av annan utrustning. Under hela körningen spänningssätts en utvald insignal. Vi kommer under större delen av detta dokument gå igenom och reda ut hur insignal, kabeldragningar och utsignaler konfigureras och samverkar.
Bombens sätt att angripa Enigma
Enigma maskinen har ett antal inställningsmöjligheter som tillsammans ger över 10 upphöjt med 20 inställningar. De olika inställningarna är:
- Tre hjul av fem används i rätt ordning ger 60 varianter
- Rätt Position för hjulen ger 17.576 varianter (26 upphöjt med 3)
- Rätt ringinställning för hjulen ger 676 varianter(26 upphöjt med 2)
- Tio korskopplingar mellan 20 av 26 möjliga bokstäver ger cirka tio upphöjt med 14 varianter
Alla dessa kombinationer är naturligtvis omöjliga att testa uttömmande. För att det skall vara möjligt att med en maskin testa sig fram krävs smarta förenklingar av Enigmas arbetssätt. Vi tar en närmare titt på hur bomben hanterar de olika typerna av inställningar för att förenkla arbetet.
Tre hjul av fem i rätt ordning.
Bomben kan i princip bara testa en uppsättning hjul i taget. Det betyder vid en första anblick att man skulle behöva köra maskinen 60 gånger för att gå igenom alla varianter. I praktiken fanns det under kriget tyska regler som begränsade antal möjligheter radikalt. Samma hjuluppsättning fick till exempel inte förekomma två gånger samma månad och ett hjul fick inte sitta i samma position två dagar i rad. De tyska begränsningarna, som naturligtvis var kryptologiskt förkastliga, gjorde arbetet betydligt enklare för dekryptörerna. För bombens skull är det hur som helst en hjulordning i taget som gäller. Därefter testas nästa hjulordning antingen på samma maskin eller parallellt på andra bomber. Bomberna massproducerades bland annat av denna anledning.
Rätt Position för hjulen.
Här görs inga förenklingar över huvudtaget. Det är verkligen så att alla 17.576 positioner testas uttömmande.
Rätt ringinställning för hjulen.
Det finns ingen hantering av olika ringinställningar i bomben. Dessa utreddes av annan utrustning som användes efter bomben. Här tycker jag att bomben har sitt största tillkortakommande. Vi chansar helt enkelt på att ingen triggning av mitthjulet stör vår bombkörning. Vi kommer diskutera ringinställningarna lite mer senare men sticker än så länge huvudet i sanden.
Tio korskopplingar mellan 20 av 26 bokstäver.
Överlägset flest variationer ger korskopplingarna som görs vid ingången till och utgången av Enigmas rotorpaket. Det gällde att få bort korskopplingarna för att uttömmande test av kombinationer skulle vara rimlig. Här kommer det första genidraget när det gäller designen av bomben. Bomben innehöll inga korskopplingar utan simulerade Enigmas enbart bestående av rotorpaketet. Hur detta var möjligt skall vi snart reda ut.
Rimligt antal kombinationer att genomsöka.
Med de förenklingar som gjorts med Enigma varianter skulle det vara möjligt att genomsöka alla. Vi har nu endast 17.576 kombinationer av rotorpositioner att testa för 60 hjulval. Ett problemet är dock att vi inte vet vad vi söker. Vi har naturligtvis en krypterad text till vårt förfogande men den ger ingen information om vad vi letar efter. Vi behöver ytterligare en komponent för att bomben skall kunna arbeta. Vi behöver ett stycke klartext, d.v.s. vi behöver en bit av texten som den såg ut innan den krypterades. Vi behöver ett pålägg (eng. crib).
Pålägg en förutsättning för bomben.
Bomben klarar sig som sagt var inte utan en bit av den icke krypterade texten. Det kan ju verka begränsande att bombens design förutsätter en del av klartexten eftersom det är den vi söker. Det är dock inte en speciellt stark begränsning. Det fanns under kriget gott om krypterade meddelande där en del av klartexten kunde gissas. Det fanns till exempel meddelande som inleddes likadant varje gång. Ett exempel är väderleksrapporter som i inledningen ofta hade med just ordet väderleksrapport (ty. Wettervorhersage). Det är väl också rimligt att anta att en hel del meddelanden avslutades med något i stil med ”Heil Hitler”. Den exakta positionen för pålägget i förhållande till den krypterade texten underlättades av att Enigma aldrig kan kryptera en bokstav till sig själv.
Inpassning mellan pålägg och kryptotext ger meny
Nu är det dags att utnyttja det gissade pålägget.
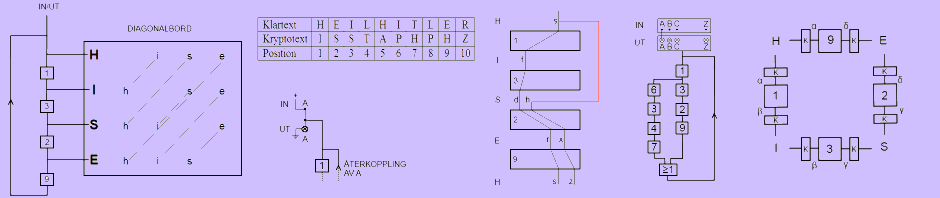
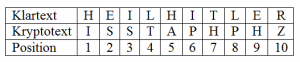
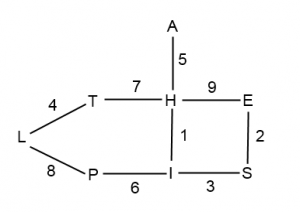
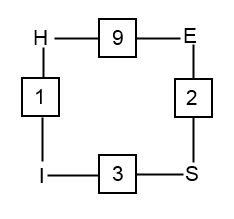
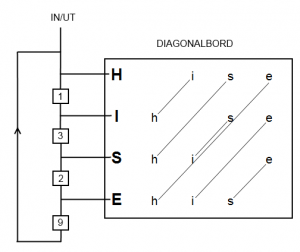
Om vi antar att vi lyckas passa in påläggets position i kryptotexten konstruerar vi en så kallad meny. I menyn bildar bokstäverna noder som sammankopplas av ”Enigma-maskiner”. Kom ihåg att efter att H krypterades till I i position 1 stegar Enigma ett steg fram innan E krypteras till S i position 2 o.s.v.
Menyn utnyttjar Enigmas inverterande egenskap, om A översätts till B så översätts B till A. Vid konstruktion av menyn behöver hänsyn därmed inte tas till vad som är klartext respektive kryptotext.
Menyns kvalitet avgörande
Menyns struktur är avgörande för om den kan användas för att sätta upp bomben eller ej. För den första versionen av bomben krävdes det att menyn innehöll slutna slingor och gärna tre stycken. När diagonalbordet (eng. Diagonal Board) tillkom var det inte längre ett absolut krav med sluten slinga i menyn men oftast behövdes en. Vi kommer behandla diagonalbordet senare. Än så länge bygger vi vidare på bomben utan diagonalbord och behöver därmed slutna slingor.
Sluten slinga av Enigma maskiner
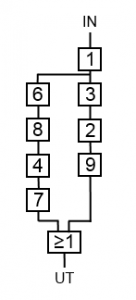
Vi börjar med att bara utnyttja den högra slutna slingan i menyn. Om vi tänker oss att vi sammankopplar fyra enigma-maskiner i positionerna 1, 3, 2 respektive 9 genom att ta utsignalen från 1 som insignal till 3 o.s.v. och därefter matar in ett H i första maskinen får vi ut ett H från sista maskinen. Inget konstigt egentligen men problemet är att vi inte vet hjulinställningen och inte heller korskopplingarna.
Samma slutna slinga utan korskoppling.
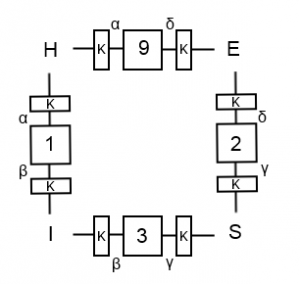
Betrakta nu följande omritning av slingan.
Vi har delat upp Enigma-maskinerna så att de består av tre delar. Första delen är en ingångskorskoppling som översätter till exempel H till α eller I till β. Andra delen är rotordelen bestående av hjul och reflektor. Tredje delen är en utgångskorskoppling som översätter till exempel α till H. Om vi nu tänker oss att vi skickar in α istället för H i maskin nummer 1 som bara består av rotordelen av Enigma-maskinen så får vi ut β. Det är ju just detta vi har i bomben, Enigma-maskiner utan korskopplingar. Om nu α är H:s korskopplingspartner kommer vi att få ut alfa efter slingan 1, 3, 2, 9. Vi kan se det som att vi kortsluter mellan de två α-tecknen i bilden, och även mellan de två β-tecknen o.s.v. Vi ritar slingan igen efter kortslutningarna.
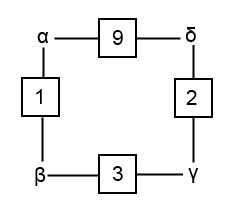
Vi har vunnit en seger, vi blev av med korskopplingarna. Priset för segern är att vi inte längre vet vilka bokstäver som ingår i menyn eftersom α, β, γ och δ är okända. Vi vet dock en viktig egenskap för de okända storheterna. Nämligen att de kommer ut som sig själva efter att ha passerat den slutna slingan. Det skall utnyttjas rejält när bomben kopplas upp.
Dags att börja koppla ihop bombens maskiner
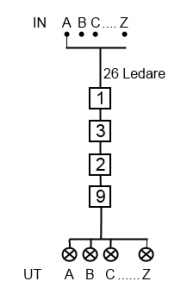
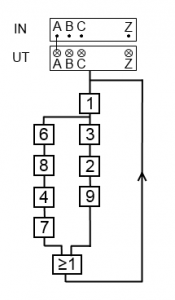
Vi kopplar nu ihop maskinerna 1, 3, 2 och 9 enligt följande schema:
Vi har alltså dragit en kabel, bestående av 26 ledare, från utsignalerna på bombens första Enigma-maskin till insignalerna på bombens tredje Enigma-maskin. Likadant har vi gjort mellan maskin tre och två samt mellan maskin två och nio.
Vi ansätter nu α lika med en bokstav, naturligtvis utan att veta om det är rätt eller ej. Vi väljer A, vilket var vad man gjorde för det mesta under kriget. A:s insignal spänningssätts. Därefter låter vi bomben prova igenom alla sina 17576 kombinationer i jakt på situationer där A:s utsignal är spänningssatt och lampan lyser. Om A lyser har vi en kandidat som kan vara rätt både avseende rotorpositioner och korskopplingspartner till H. Detta gör att bomben stannar och kandidaten testas vidare med annan utrustning.
Än så länge är dock inte maskinen speciellt effektiv. Om vi har fel korskopplingspartner eller rotorställning kommer ändå någon utsignal vara spänningssatt, för det mesta någon annan bokstav men i ungefär vart 26 fall A. Vi kommer alltså få en orimlig mängd falska stopp, ungefär 17576/26 d.v.s. 676 stycken. Detta får vi oavsett om vi valt rätt korskopplingskamrat eller ej. Vi behöver tillföra ytterligare kopplingar till maskinen för att den skall bli möjlig att använda. Vi tar nu användning av den andra slingan i menyn.
Flera slingor i samverkan
Om vi nu kopplar upp även den vänstra slingan i menyn får vi följande totalschema.
Lägg märke till att den första Enigma-maskinen används i båda slingorna i analogi med hur det ser ut i menyn. Vi har dessutom lagt till ”eller”-funktion på utsignalerna vilket innebär att lampa A lyser om någon av slingorna genererar ett A. Detta innebär att två lampor kan lysa samtidigt. Vi omformulerar nu stoppkravet på maskinen. Nu kräver vi att båda slingorna ger utsignal A för insignal A, det vill säga vi stoppar bara maskinen om lampa A lyser ensam.
Nu reduceras antalet falska stopp rejält. Eftersom båda slingorna måste generera falskt A oberoende av varandra kommer bara var 26*26 = 676 rotorposition att generera falskt stopp. Totalt har vi därmed fått ner antalet falskstopp till cirka 17576/676 d.v.s. 26 stycken.
Nu kan vi på allvar inse vad menykvalité betyder. Om vi haft tillgång till en tredje slinga hade antalet falska stopp kommit ner till riktigt trevlig nivå, kanske ett eller några stycken.
Vi har nu fått ner antalet falskstopp till en rimlig nivå förutsatt att vi lyckas konstruera en meny av god kvalité. Men vi har fortfarande kvar problemet att vi kan ha valt fel insignal A som korskopplingspartner till H. Vi ska nu lägga till ytterligare kopplingar som gör att vi kan hitta rätt lösning även om korskopplingsantagandet är felaktigt.
Återkoppling av utsignalerna
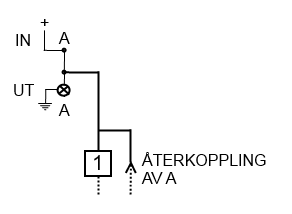
Vi har nu återkopplat utsignalen till insignalen. Vi har dessutom flyttat upp utsignalerna nära insignalerna men detta betyder inget för funktionen. Jag förtydligar logiken i övre delen av bilden genom att rita ytterligare en bild. Den elektriska kretsen för signal A kan realiseras som i figuren nedan. Vi har naturligtvis motsvarande kretsar för alla 26 signaler (fast utan spänningssättning). Lägg märke till att vi nu bara ritar en av de 26 ledarna i, till exempel, återkopplingen.
Om vi spänningssätter A:s insignal kommer lampan lysa. Dessutom kommer insignalen skickas in i slingorna av Enigma-maskiner. Om alla slingorna har utsignal A kommer denna att återkopplas och inget mer händer. Vi har ett stopp.
Om däremot minst en av slingorna har en annan utsignal än A kommer denna att återkopplas och tända motsvarande lampa samt spänningssätta dess insignal till slingorna. Ytterligare utsignaler kommer då att återkopplas o.s.v. Om vi har en felaktig rotorställning är det högst sannolikt att alla lampor kommer tändas om vi använder en bra meny. Om alla lamporna tänds kan vi inte ha rätt rotorställning och låter maskinen köra vidare. Om däremot inte alla lampor tänds betraktar vi det som en möjlig kandidat och maskinen stoppar.
Återkopplingen av utsignalen har stor betydelse om korskopplingspartnern är felaktig. Om vi har fel korskopplingsansats men når fram till rätt rotorställning kommer detta till att leda till ett stopp eftersom den rätta korskopplingspartnern har en isolerad krets vid rätt rotorställning. Sannolikt kommer alla andra signaler att spänningssättas men inte den korrekta partnern.
Sammanfattningsvis kan man säga att det inte spelar någon roll om vi valt rätt korskopplingsansats eller ej. Vi kommer att få den korrekta partnern och rätt rotorställning vid ett av stoppen. Vi kommer sannolikt ha mer än ett stopp att prova vidare men antalet kommer att vara hanterbart. Återigen vill jag påminna om att vi är beroende av kvalitén på menyn för att få ner antalet falska stopp till en rimlig nivå.
Flera slingor och återkoppling i samverkan
Vi har nu kommit en bra bit med bygget av bomblogiken. För att ytterligare förklara vad vi åstadkommit tar vi hjälp av följande bild.
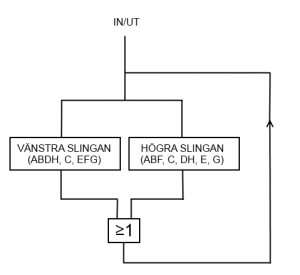
Jag har ritat två slutna slingor från en meny och återkoppling. Jag har tagit mig friheten att klumpa ihop alla Enigma-maskiner i respektive slinga. I bilden har jag dessutom lagt till den permutation av bokstäverna som respektive slinga gör för en viss rotorställning. För att förenkla bilden låtsas jag tillfälligt att vårt alfabet bara innehåller åtta bokstäver.
Betrakta vänstra slingans permutation (ABDH, C, EFG). Det betyder att den vänstra slingans maskiner tillsammans omvandlar ett A till B, B till D, D till H och H till A. Vidare omvandlas E till F, F till G och G till E. C omvandlas till sig själv vilket är helt okej eftersom vi har en slinga av Enigmor, inte bara en maskin. Högra slingan har permutationen (ABF, C, DH, E, G) vilket bland annat betyder att C, E och G omvandlas till sig själv.
Om vi spänningssätter C på insignalen så kommer båda slingorna att omvandla C till C. Återkopplingen kommer återkoppla spänning på C och inget mer händer.
Om vi spänningssätter A på ingången kommer båda slingorna omvandla A till B. Återkopplingen av B kommer tända lampa B samt spänningssätta B på båda slingornas ingångar. Vänstra slingan omvandlar B till D och högra slingan omvandlar B till F. Återkopplingen av D och F kommer att tända lamporna D och F samt spänningssätta D och F på båda slingornas ingångar. Nästa varv spänningssätts G och H. Varvet därefter spänningssätts även E. Alla lampor utom C kommer att lysa.
Kontrollera gärna själv att alla lampor utom C hade lyst oavsett vilken korskopplingspartner vi valt förutom C.
Om vi nu antar att denna rotorställning är den korrekta kommer vi att får C som antingen den enda som lyser eller den enda som inte lyser. Detta kommer att få bomben att stoppa och vi kommer att undersöka denna rotorställning och C som korskopplingspartner vidare.
Återigen vill jag påminna om att det inte finns någon som helst garanti för att detta är rätt varken när det gäller rotorställning eller korskopplingspartner. Det kan mycket väl vara så att fel hjul som sitter i maskinen eller att vår meny inte är av tillräckligt hög kvalité utan ger ett slumpmässigt stopp.
Första versionen av bomben är konstruerad
Detta är den funktionalitet som den första versionen av Turing Bomb innehöll. Det gick att få fram ett begränsat antal kandidater för vidare prövning genom att koppla upp maskinen med menyns slingor samt återkoppling. Maskinen körde sedan igenom alla 17576 rotorkombinationer i jakt på kandidater.
Första maskinen togs i bruk på Bletchley Park under våren 1940. Det stod dock klart redan då att ytterligare innovationer behövdes för att maskinen skulle bli en riktigt effektiv kodknäckare.
Brister i första versionen av bomben
Första versionen av bomben hade en uppenbar brist. Den krävde menyer av väldigt hög kvalité. Det är inte lätt att få ihop menyer som innehåller tre slingor. Även om man har ett rejält långt pålägg så kan man inte använda hur många Enigma-maskiner som helst i menyerna eftersom man då högst sannolikt råkar ut för att högerhjulet triggat mitthjulet i den krypterande Enigma-maskinen. Kom ihåg att vi inte klarar av att ha en mitthjulsändring inom vår meny. I praktiken kan vi därför inte använda pålägg som är längre än cirka tolv positioner.
Diagonalbord läggs till
En fullkomligt lysande innovation tillkom när andra versionen av bomben designades. Diagonalbordet (en. Diagonal Board) som det kallas är så betydelsefullt att dess uppfinnare Gordon Welchman ibland fått vara med och ge namn åt bomben tillsammans med Alan Turing.
Återkopplingen som vi tillfört bomben spelar som vi såg innan ingen större roll om vi väl hittat rätt hjulval, rotorställning och korskopplingspartner. Det är istället när någon eller några av inställningarna är fel som den gör nytta. Jag brukar tänka att dess uppgift är att sprida spänningssättningen så mycket som möjligt i maskinen. Vi behöver ju inte vara rädda att förstöra en korrekt inställning eftersom att då är ju den korrekta slingan isolerad från omvärlden. Detta gäller även för diagonalbordet, den skall sprida spänningssättningen så mycket som möjligt men riskerar inte att förstöra en korrekt inställning.
För att förklara diagonalbordets princip backar vi tillbaks till vår första uppkoppling av bomben där vi bara använde den högra slingan. Vi låtsas för en liten stund dessutom att vi bara har fyra bokstäver i vårt alfabet (H, I, S och E) vilket gör diagonalbordet lättare att rita.
Från insignalerna på första Enigma-maskinen drar vi en kabel med 4 ledare till bokstaven H på diagonalbordet eftersom H fanns på insignalen på menyn. Vi gör motsvarande med de andra bokstäverna. Inom diagonalbordet korskopplas alla bokstäver så att till exempel s-ledaren vid H kopplas ihop med h-ledaren vid S.
Om nu S är spänningssatt vid ingången till första Enigma-maskinen så kan vi ha ett av följande två fall:
- S är den sanna korskopplingspartnern till H
- S är inte den sanna korskopplingspartnern till H
Om S är korskopplingspartner till H så skall även H vara spänningssatt vid ingången till Enigma-maskin nummer två eftersom där står S i menyn. Observera att Enigma-maskin nummer två är näst nederst i bilden. Om rotorställningen är korrekt kommer i själva verket diagonalbordet inte tillföra något eftersom slingan spänningssätter H vid ingången till Enigma-maskin nummer två. Om rotorställningen däremot är inkorrekt gör diagonalbordet högst sannolikt nytta genom att sprida spänningssättningen.
Om S inte är korskopplingspartner med H gör högst sannolikt diagonalbordet nytta såväl vid korrekt rotorställning som vid inkorrekt. Om rotorställningen är korrekt vill vi gärna sprida spänningssättningen så mycket som möjligt förutom för den ”korrekta” slingan. H ingår inte i den korrekta slingan vid ingången till Enigma-maskin nummer två eftersom H inte är korskopplingspartner med S och därför spänningssätter vi gärna H där. Om rotorställningen är inkorrekt vill vi åter igen sprida spänningssättningen.
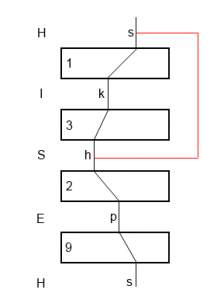
Jag vill ytterligare belysa logiken som diagonalbordet tillför. Betrakta följande bild.
Bilden skall tolkas som att vi valt S som korskopplingspartner till H och den spänningssatta vägen genom slingan går via s=>k=>h=>p=>s. Vi har en rotorställning där S som korskopplingspartner till H åtminstone inte kan förkastas av det vi ser i bilden. S kommer ut som S vilket verkar lovande. Inte heller diagonalbordet kan avslöja några oegentligheter. Enda diagonalkopplingen som är relevant är ju den mellan s ledaren vid H och h ledaren vid S. Denna diagonalkoppling tillför inget eftersom slingan själv spänningssatt s vid H och h vid S.
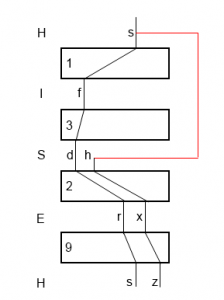
Betrakta nu följande bild.
Även här verkar det ju lovande genom att S kommer ut som S ur slingan via vägen s=>f=>d=>r=>s. I detta fallet agerar dock diagonalbordet väktare och avslöjar ställningen som icke möjlig lösning. Genom att samma diagonalkoppling som tidigare kortsluter mellan s vid H och h vid S kommer en ny signal z att vara spänningssatt vid slingans utgång. Detta betyder att både S och Z återkopplas, tänder sina lampor och Z spänningssätts på ingången till slingan och lavinen är igång.
En trevlig egenskap som diagonalbordet har är att det även utnyttjar Enigmor som inte är med i någon sluten slinga. Från vår meny hade vi även kunnat utnyttja bokstaven A och Enigma nummer 5, trots att de inte ingår i någon sluten slinga, eftersom A då blivit diagonalkopplat precis som alla andra bokstäver från menyn. Diagonalbordet har därmed löst problemet med att finna tillräckligt bra menyer att mata bomben med. Vi klarar oss i allmänhet med en sluten slinga.
Schack Matt Enigma
Avslutning
I Maj 2012 besökte jag Bletchley Park under två dagar. På museet finns den kopia av Bomben som byggts under senare år. Bomben var ganska ny för mig och jag visste inte riktigt hur den fungerade men blev genast betagen av den. Det har tagit mig massvis av timmar för att fullt ut förstå maskinens genialitet.
Med detta vill jag ge tröst åt dig om du har läst dokumentet och känner dig lite förvirrad. Ge inte upp, läst det igen eller komplettera med något från litteratur- och länklistan. Jag lovar, det är värt det.
/Peter
Litteratur och länkar
Det finns en separat sida med länkar.